Introduction

Waves propagating through the Earth are always affected by anisotropy to some degree. Banik (1984), Kaarsberg (1959), Podio et al. (1968) and Jones and Wang 1981) have discussed the anisotropic behaviour of shale formations on the wave propagation. Shale is the dominant rock type found in many sedimentary basins of the world (Annamalai et al. 2015). All seismic data, including the seismic velocities, are affected by the anisotropic properties of these rocks. Seismic velocities and well velocities have always been used to predict the depth of the target formations. Seismic velocities have mostly been found to overestimate depth and usually modelled using check-shot or well velocities for a better calibration with depth. Seismic velocities are generally non-normal velocities which contain part of the horizontal component and higher than the well velocities (Banik 1984). The anisotropy values cannot be extracted by only using seismic data, so well velocities or VSP data are used in most cases. Even when the anisotropic values are extracted, it is usually of low resolution and shows effective anisotropy over large depths. For higher resolution, well data are frequently used. This paper discusses the use of both vertical and deviated wells to derive the Thomsen’s anisotropic parameters with better resolution. Annamalai et al. (2015) and Sayers et al. (2015) have derived the anisotropic parameters by comparing vertical and deviated velocity. In the absence of vertical well, the vertical velocity is predicted through kriging method (Sayers et al. 2015) or by other statistical assumption (Annamalai et al. 2015). In this study, calibrated Gardner’s equation (Gardner et al. 1974) is used to predict both the vertical compressional and shear velocity, which is further used to predict the Thomsen’s anisotropic parameters. The workflow is shown in Fig. 1.

Fig. 1
figure 1

Workflow to extract Thomsen’s anisotropic value from a deviated well

Full size image

Study area

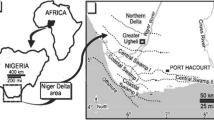
The study area lies in the Mahanadi Basin, East coast of India. Sedimentation to this basin started with the breakup of Antarctica during the Early Cretaceous period (Nemcok et al. 2013). The sedimentation is mainly fed by the Ganga–Brahmaputra river, Brahmani and Subarnarekha river system (Roy et al. 2015), in the order of 7.10 × 109 kg/year (Subrahmanyam et al. 2008). The drainage area of Ganga and Brahmaputra rivers is about 1,060,000 km2 and 630,000 km2, respectively (Gansser 1964). In this study area, 10 wells were drilled in the shallow water geological set-up (John et al. 2014; Kumar et al. 2015) and intersected through Plio-Pleistocene to Miocene deltaic shallow marine shale with sandstone–siltstone intercalations, where the Miocene shale formations exhibited abnormally higher overpressure up to > 19.7 Mpa/km.

Literature

Shales are generally considered to be transversely isotropic (Vernik and Nur 1992); under normal condition of a simple depositional structure, a VTI model can be assumed with a vertical symmetry axis. It means the velocity measured at the symmetry plane shall be constant but when measured vertically or along the symmetry the values may be different. Velocity is a vector quantity; it gets polarized in different axis as shown in Fig. 2. The velocities measured along the symmetry axis are the \(v_{p0} \,\& \,V_{s0}\) (compressional and shear wave velocities). In this study, it has been assumed that the recorded sonic velocities are phase velocities (Ellefsen et al. 1989). Thomsen’s equations are used for weak anisotropy. The S wave, when polarized perpendicular to the symmetry, is called \(V_{SH}\), and parallel to the symmetry is \(V_{sV}\). The propagation direction of \(V_{sV} \,\& \,V_{s0}\) is same, so they are equal in TI geometry. The P wave polarized in the horizontal direction is represented as \(V_{pH}\). For the VTI model, analysis of elastic tensor contains five independent components, which are

$$C_{IJ} = \left( {\begin{array}{*{20}c} {c_{11} } & {c_{12} } & {c_{13} } & 0 & 0 & 0 \\ {c_{21} } & {c_{11} } & {c_{13} } & 0 & 0 & 0 \\ {c_{13} } & {c_{13} } & {c_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {c_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {c_{44} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {c_{66} } \\ \end{array} } \right) ,$$

where \(c_{12} = c_{21} = c_{11} - 2c_{66} .\)

Fig. 2
figure 2

Model to show polarization of velocities in a different direction for TI media. SV is the shear wave in the vertical direction, SH is the shear wave in the horizontal direction, and PH is the compressional wave in the horizontal direction

Full size image

In general, the values of elastic constant are not measured, but the velocities are measured in a different direction. So, the distinction is required at this level between the phase and the group velocities shown in Fig. 3. Phase velocity is the velocity of the mono-frequency plane wave, while group velocity is the velocity of energy propagation along a ray path (Hemsing 2007). Hence, the phase velocity is x2/time and group velocity is x1/time. Under the isotropic environment, the wavefront is circular (x1 = x2). However, in the anisotropic condition, the velocities at different angles will be different. Musgrave (1970) considered the equation of motion for anisotropic media connecting the elastic coefficient and velocity of the matrix which is as follows:

$$\left( {C_{ijkl} n_{j} n_{l} - \rho \nu^{2} \delta_{ik} } \right)p_{k} = 0,$$

where \(C_{ijkl}\) are elastic coefficient, \(n_{j}\) and \(n_{l}\) are components of the wavefront normal, \(\rho\) is the density, \(\nu\) is the phase velocity, \(\delta\) is the Kronecker delta function and \(p\) is the unit displacement vector, commonly written as \(\left( {\varGamma_{ik} - \rho \nu^{2} \delta_{ik} } \right)p_{k} = 0\), and \(\varGamma\) is the Christoffel matrix. This eigenvalue problem shall lead to three mutually orthogonal polarized phase velocities. Generally, these waves are not polarized perfectly with respect to the propagation direction and thus are often referred to as quasi-P waves (qP) and quasi-S waves (qS). In a medium of TI symmetry, the phase velocities are given as follows (Thomsen 1986):

$$v_{p} \left( \theta \right) = \left( {\frac{{c_{11} \sin \left( \theta \right)^{2} + c_{33} \cos \left( \theta \right)^{2} + c_{44} + \sqrt M }}{2\rho }} \right)^{{\frac{1}{2}}}$$
$$v_{sV} \left( \theta \right) = \left( {\frac{{c_{11} \sin^{2} \left( \theta \right) + c_{33} \cos^{2} \left( \theta \right) + c_{44} - \sqrt M }}{2\rho }} \right)^{{\frac{1}{2}}}$$
$$v_{sH} \left( \theta \right) = \left( {\frac{{c_{66} \sin^{2} \left( \theta \right) + c_{44} \cos^{2} \left( \theta \right)}}{\rho }} \right)^{{\frac{1}{2}}} ,$$

where

$$M = \left\{ {\left( {c_{11} - c_{44} } \right)\sin \left( \theta \right)^{2} - \left( {c_{33} - c_{44} } \right)\cos \left( \theta \right)^{2} } \right\}^{2} + \left( {c_{11} + c_{44} } \right)^{2} \sin \left( {2\theta } \right)^{2} .$$
Fig. 3
figure 3

Difference between the phase and group velocity. The distance from the origin (o) to R1 and R2 point is different, so the phase and the group velocities will be different

Full size image

Using the above equation, five independent elastic constants were derived which are

$$c_{11} = \rho v_{pH}^{2} ,\quad c_{33} = \rho v_{p0}^{2} ,$$
$$c_{44} = \rho v_{s0}^{2} ,\quad c_{66} = \rho v_{sH}^{2} \quad {\text{and}}$$
$$c_{13} = \left[ {\frac{{\left( {4\rho v_{{p_{45} }}^{2} - c_{11} - c_{33} - 2c_{44} } \right)^{2} - \left( {c_{11} - c_{33} } \right)^{2} }}{4}} \right]^{{\frac{1}{2}}} .$$

Thomsen (1986) defined three parameters for the characterization of weak anisotropy of a transversely isotropic material:

$$\varepsilon = \frac{{c_{11} - c_{33} }}{{2c_{33} }},\quad \gamma = \frac{{c_{11} - c_{33} }}{{2c_{33} }} ,\quad \delta = \frac{{\left( {c_{13} + \frac{{c_{44} }}{2}} \right)^{2} - \left( {c_{33} - \frac{{c_{44} }}{2}} \right)^{2} }}{{2c_{33} \left( {c_{33} - \frac{{c_{44} }}{2}} \right)}},$$

where ε and γ describe the anisotropy properties of the compressional and shear waves, respectively.

Replacing them in the equation under weak anisotropy approximation leads to

$$v_{qP} \left( \theta \right) \cong v_{{P_{0} }} (1 + \delta \sin^{2} \theta \cos^{2} \theta + \varepsilon \sin^{4} \theta )$$
$$v_{qSv} \left( \theta \right) \approx v_{S0} \left[ {1 + \left( {\frac{{v_{P0} }}{{v_{S0} }}} \right)^{2} \left( {\varepsilon - \delta } \right)\sin^{2} \theta \cos^{2} \theta } \right]$$
$$v_{SH} \left( \theta \right) \cong v_{S0} (1 + \gamma \sin^{2} \theta ) .$$

Methods

The above equations are used to derive the anisotropic parameters in this study. Huge sedimentation of impervious claystone in the study area is assumed to be the source of anisotropy. To extract anisotropy of the sediments, monopole (axisymmetric) transducers were used to record sonic velocities and exported after standard sonic processing and corrections. Sonic velocity recorded in this deviated well varies from 5° to 55° from the normal and is thus assumed to be affected by the anisotropy of the matrix. The referenced vertical velocities were obtained from the nearby wells. Initially, relative changes in sonic velocities from its vertical counterpart along the well deviation are used to derive the anisotropic values at different zones. However, due to heterogeneity in the system, the results were erroneous even when comparing velocities from two nearby wells directly. Hence, vertical velocity was derived from bulk density log at the deviated well location using a calibrated Gardner empirical equation.

Density–velocity relation

Density being isotropic does not depend upon the direction of measurement and can be used to predict the isotropic velocity at the desired depths. Three nearby wells were used to deduce the Gardner relation between the density and velocity. Since the anisotropy is mainly associated with clay, well data were filtered for clay and only those points of density and velocity are selected where the clay is more than 80%. The vertical portion of the deviated well was also used, and an empirical equation was derived based on Gardner equation as shown in Fig. 4. This relationship was blind-tested in the nearby vertical wells, which suggest that the predicted velocity is matching well with the recorded velocity (Fig. 5). Further, the relationship was used on the deviated portion of the deviated well to predict the vertical velocity (V0) from density varying with depth.

Fig. 4
figure 4

Vp–density empirical relationship for the location (calibrated Gardner equation)

Full size image
Fig. 5
figure 5

Predicted velocity (green) overlaid on recorded velocity (red) for two nearby vertical wells

Full size image

Anisotropy estimation

The sonic velocity which is recorded in a deviated well is generally higher than its vertical counterpart in the presence of anisotropy. If the sonic velocity used uncorrected, it would lead to some error in the resultant estimations, such as an error in the pore pressure estimation, velocity modelling or time–depth conversion. Predicted velocity using the calibrated Gardner equation shows us the impact of deviation on the velocity prediction. Thomsen’s parameters are used to correct the deviated sonic well log data. Figure 6 shows that the recorded sonic velocity is higher than the predicted vertical velocity as the well deviation increases. This difference in the velocities is used to calculate the Thomsen’s anisotropic parameters zone wise, whereas these zones are defined based on seismic reflection pattern (Fig. 7) and represent a similar depositional environment. Anisotropy is assumed to be constant within the zone. Thomsen’s equations are fitted to derive epsilon and delta, minimizing the fitting RMS error (Table 1). The impact of anisotropy is negligible in the sand units, so not considered here. If weak anisotropy is not assumed, extracted anisotropic values using the exact solution shall be as shown in Table 2.

Fig. 6
figure 6

Compressional velocities plot against well deviation. The green curve on the upper figure is the predicted vertical velocity. The green curve in the lower figure is the vertical velocity after applying the Thomsen’s anisotropy values

Full size image
Fig. 7
figure 7

Zones for extraction of anisotropy were defined by the seismic reflection pattern. Four zones are defined

Full size image
Table 1 Anisotropic values extracted along the well in different zones assuming weak anisotropy
Full size table
Table 2 Anisotropic values extracted along the well in different zones using the exact solution
Full size table

Synthetic seismic

Thomsen’s parameters ε, δ and γ extracted in the previous section are interpolated and isotropic, and an anisotropic synthetic gather is generated. Pick analysis of the actual seismic gather at the well location and both the synthetic seismic are overlaid over each other. The crooked blue curve (Fig. 8) represents the variation of amplitude across the different angles in the pre-stack time (PSTM)-migrated seismic gather data, the yellow curve fitting represents the conventional AVO model using uncorrected sonic velocity, the red curve fitting represents the AVO 2 terms, and the black curve fitting represents the anisotropic AVO model using the above-derived Thomsen’s parameters. The well logs along with the interpolated anisotropic Thomsen’s parameters are used to generate the isotropic and the anisotropic AVO response. Ignoring the impact of anisotropy shall lead to spurious AVO response and right model is not possible without the inclusion of vertical and horizontal variation of the wave velocities.

Fig. 8
figure 8

The blue line is the actual variation of amplitude in seismic gather. The ‘Red’ line is the AVO 2 terms fitting. The ‘Greenish Yellow’ line is the conventional AVO model using in situ well logs. The black line is the anisotropic AVO model using derived Thomsen’s parameter

Full size image

Mineralogy within the subsection

Intrinsic anisotropy of the shales is mainly due to the presence of phyllosilicate minerals which seldom occur more than 70% in any shales (Katahara 1996). Plate-like clay particles are aligned and create inter-particle crack-like pores. These pores containing water may change the elastic properties of the clay minerals. Dry velocities of the clay minerals (illite, chlorite and kaolinite) are the same, but the wet properties vary widely depending on the surface area and volume of associated adsorbed water (Katahara 1996). The amount of incorporated water is different for different clays. The volume of water incorporated in a smectite mineral is five times the volume incorporated by an illite mineral (Katahara 1996). Thus, smectite elastic properties are different than illite and chlorite, which absorb less water. Kaolinite, on the other hand, shows higher C13 and C44, which leads to +ve delta values. Table 3 shows the presence of chlorite and illite minerals which can reduce the ‘Delta’ to negative values. About 49 cutting samples from Well 1 were used for the XRD analysis in the depth ranging from 910 to 2020 m. Figure 9 shows the XRD results and the distribution of clay minerals in the different zones.

Table 3 Thomsen’s anisotropy parameters calculated using the data published in Katahara (1996)
Full size table
Fig. 9
figure 9

Well 1 XRD results of multiple samples from different zones defined in Fig. 7

Full size image

Results and discussion

The velocity–density cross-plot suggests a strong relationship with R2 greater than 80%. The filtering of data based on similar lithology has significantly improved the correlation coefficient. The predicted vertical velocity at different depths gave an excellent control to run the inversion to fit VTI model into the deviated well data. Assuming constant anisotropic value, the total drilled well section is divided into multiple zones guided by seismic reflection patterns such that each zonation represents a similar depositional environment. Zone 2 has a negative delta, which may be the result of the presence of high chlorite and illite in the matrix, as shown in Fig. 9. Katahara (1996) and Bayuk et al. (2007) have also noted similar observations. Elastic properties of water-saturated smectite and kaolinite do not contribute to negative delta. Well tie was performed using an in situ isotropic synthetic gather and zero-offset VSP. The amplitude across the angle (AVA) in the synthetic gather showed a much gentler amplitude gradient in comparison with recorded seismic gather. An anisotropic gather generated using the interpolated delta and epsilon well log shows a more realistic AVA behaviour at the reservoir. Anisotropic values for delta (δ) are also derived using zero-offset VSP velocities and seismic PSDM velocities, as shown in Table 4. When compared with the well-derived anisotropic delta values, results using seismic velocities are different and substantially low. This is probably because seismic derived anisotropic values are more representative of effective anisotropy, rather than intrinsic anisotropy of rocks.

Table 4 Thomsen’s anisotropy parameter delta (δ1 and δ2) derived using VSP and seismic raw and calibrated PSDM velocities, respectively
Full size table

Conclusion

Clay-rich fine layering with intercalated sand and shale encountered in the Mio-Pliocene sediment is the primary reason for seismic anisotropy in this well. These uncorrected sonic velocities in the deviated well may result in unrealistic pore pressure estimation and time–depth conversion. Hence, these sonic velocities recorded in a deviated well need to be corrected before it is being used for any other purpose.

Calibrated Gardner equation was used to estimate the vertical velocities from the bulk density log. The anisotropy values are further related to the presence of various clay minerals observed within the identified zonations. XRD clay mineralogy data show a possible relation between the high presence of chlorite and illite and sign of delta. The sign of delta remains the same using exact solution as well as in weak anisotropy assumption. The anisotropic values extracted are further used to derive better fitted AVO curves in pre-stack gather. Thomsen’s parameter deduced through this process can be further used to model seismic response, pore pressure and time–depth calibration.