Skip to main content
SpringerLink
Log in

Approximation solution of the squeezing flow by the modification of optimal homotopy asymptotic method

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

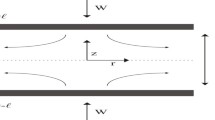
The approximate solution of the squeezing axisymmetric fluid flow between infinite plates is discussed in the present paper. An optimal homotopy analysis method with a modification function technique is proposed to solve a class of nonlocal boundary value problems, namely squeezing axisymmetric fluid flow equation. We first transform the nonlocal boundary value problems into an equivalent integral equation, and then the optimal homotopy analysis technique is utilized for an approximate solution. The numerical results confirm the reliability of the present method as it tackles such nonlocal problems without any limiting assumptions. The proposed method is tested upon squeezing axisymmetric fluid flow equation from the literature and the results are compared with the available approximate solutions including perturbation method (Ran et al. in Commun Nonlinear Sci Numer Simul, 2007. https://doi.org/10.1016/j.cnsns), homotopy perturbation method (Ran et al. 2007), homotopy analysis method (Ran et al. 2007), and optimal homotopy asymptotic method (Idrees et al. in Math Comput Model 55:1324–1333, 2012). The convergence and error analysis of the proposed method is discussed. It can be said that squeezing the axisymmetric fluid flow equation exists in different dynamical behaviors. In addition, the physical behaviors of these new exact solutions are given with two and three-dimensional graphs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. T.C. Papanastasiou, G.C. Georgiou, A.N. Alexandrou, Viscous Fluid Flow (CRC Press, Boca Raton, FL, 1994)

    MATH  Google Scholar 

  2. A.K. Al-Hadhrami, L. Elliott, D.B. Ingham, A new model for viscous dissipation in porous media across a range of permeability values. Transp. Porous Media 49, 265–289 (2002)

    MathSciNet  Google Scholar 

  3. A.K. Al-Hadhrami, L. Elliot, D.B. Ingham, Combined free and forced convection in vertical channels of porous media. Transp. Porous Media 53, 117–122 (2003)

    MathSciNet  Google Scholar 

  4. D.S. Chauhan, A. Olkha, Slip flow and heat transfer of a second grade fluid in a porous medium over a stretching sheet with power-law surface temperature or heat flux. Chem. Eng. Commun. 198, 1129–1145 (2011)

    Google Scholar 

  5. R.H. Rand, D. Armbruster, Perturbation Methods, Bifurcation Theory and Computer Algebric (Springer, Berlin, 1987)

    MATH  Google Scholar 

  6. G.L. Liu, Weighted residual decomposition method in nonlinear applied mathematics, in Proceeding of the 6th Congress of Modern Mathematics and Mechanics, Suzhou, China (1995)

  7. X.J. Ran, Q.Y. Zhu, Y. Li, An explicit series solution of the squeezing flow between two infinite parallel plates. Commun. Nonlinear Sci. Numer. Simul. (2007). https://doi.org/10.1016/j.cnsns

    Article  Google Scholar 

  8. R.J. Grimm, Squeezing flows of Newtonian liquid films, an analysis including fluid inertia. Appl. Sci. Res. 32, 149 (1976)

    ADS  Google Scholar 

  9. M.J. Stefan, Versuch Uber die scheinbare adhesion. Akad. Wiss. Math.-Natur. 69, 713 (1874)

    Google Scholar 

  10. O. Reynolds, On the theory lubrication. Trans. R. Soc. 177, 157 (1886)

    ADS  Google Scholar 

  11. F.R. Archibald, Load capacity and time relations in squeeze films. Trans. ASME J. Lubr. Technol. Soc. 32, 149–166 (1956)

    Google Scholar 

  12. Q.K. Ghori, M. Ahmed, A.M. Siddiqui, Application of homotopy perturbation method to squeezing flow of a Newtonian fluid. Int. J. Nonlinear Sci. Numer. Simul. 8(2), 179–184 (2007)

    Google Scholar 

  13. M. Idrees, S. Islam, S.I.A. Tirmizi, S. Haqa, Application of the optimal homotopy asymptotic method for the solution of the Korteweg–de Vries equation. Math. Comput. Model. 55, 1324–1333 (2012)

    MathSciNet  MATH  Google Scholar 

  14. W.A. Wolf, Squeeze film pressures. Appl. Sci. Res. 14, 77–90 (1964)

    Google Scholar 

  15. D.C. Kuzma, Fluid inertia effects in squeeze film. Appl. Sci. Res. 18, 15–20 (1967)

    Google Scholar 

  16. S. Ishizawa, Squeezing flows of Newtonian liquid films an analysis include the fluid Interia. Appl. Sci. Res. 32, 149–166 (1976)

    Google Scholar 

  17. J. Tichy, W.O. Winner, Inertial considerations in parallel circular squeeze film bearings. Trans. ASME J. Lubr. Technol. Soc. 92, 588–592 (1970)

    Google Scholar 

  18. C.Y. Wang, L.T. Watson, Squeezing of a viscous fluid between elliptic plates. Appl. Sci. Res. 35, 195–207 (1979)

    MathSciNet  MATH  Google Scholar 

  19. R. Usha, R. Sridharan, Arbitrary squeezing of a viscous fluid between elliptic plates. Fluid Dyn. Res. 18, 35–51 (1996)

    ADS  Google Scholar 

  20. A.H. Nayfeh, Introduction to Perturbation Techniques (Wiley, Hoboken, 1979)

    MATH  Google Scholar 

  21. M. Tatari, M. Dehgan, The use of the adomian decomposition method for solving multipoint boundary value problems. Phys. Scr. 73, 672–676 (2006)

    ADS  Google Scholar 

  22. M. Dehghan, J. Manafian, A. Saadatmandi, Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer. Methods Partial Differ. Equ. J. 26, 448–479 (2010)

    MathSciNet  MATH  Google Scholar 

  23. M. Dehghan, J. Manafian, A. Saadatmandi, The solution of the linear fractional partial differential equations using the homotopy analysis method. Z. Naturforsch. 65a, 935–949 (2010)

    ADS  MATH  Google Scholar 

  24. M. Dehghan, J. Manafian, The solution of the variable coefficients fourth-order parabolic partial differential equations by homotopy perturbation method. Z. Naturforsch. 64, 420–430 (2009)

    ADS  Google Scholar 

  25. J.H. He, Variational approach to the sixth-order boundary value problems. Appl. Math. Comput. 143, 537–538 (2003)

    MathSciNet  MATH  Google Scholar 

  26. M. Dehghan, J. Manafian, A. Saadatmandi, Application of semi-analytic methods for the Fitzhugh–Nagumo equation, which models the transmission of nerve impulses. Math. Methods Appl. Sci. 33, 1384–1398 (2010)

    MathSciNet  MATH  Google Scholar 

  27. M. Dehghan, J. Manafian, A. Saadatmandi, Application of semi-analytical methods for solving the Rosenau–Hyman equation arising in the pattern formation in liquid drops. Int. J. Numer. Methods Heat Fluid Flow 22, 777–790 (2012)

    MathSciNet  MATH  Google Scholar 

  28. M. Dehghan, J. Manafian, A. Saadatmandi, Application of semi-analytical methods for solving the Rosenau–Hyman equation arising in the pattern formation in liquid drops. Int. J. Numer. Methods Heat Fluid Flow 22, 537–553 (2012)

    MathSciNet  MATH  Google Scholar 

  29. M. Dehghan, J. Manafian Heris, Study of the wave-breaking’s qualitative behavior of the Fornberg–Whitham equation via quasi-numeric approaches. Int J. Numer. Methods Heat Fluid Flow 21, 736–753 (2011)

    Google Scholar 

  30. M. Moosavi, M. Momeni, T. Tavangar, R. Mohammadyari, M. Rahimi-Esbo, Variational iteration method for flow of non-newtonian fluid on a moving belt and in a collector. Alex. Eng. J. 55, 1775–1783 (2016)

    Google Scholar 

  31. J. Manafian, Solving the integro-differential equations using the modified Laplace adomian decomposition method. J. Math. Ext. 6, 1–15 (2012)

    MathSciNet  Google Scholar 

  32. B. Parsa, M.M. Rashidi, O.A. Bég, S.M. Sadri, Semi-computational simulation of magneto-Hemodynamic flow in a semi-porous channel using optimal homotopy and differential transform methods. Comput. Bio. Med. 43, 1142–1153 (2013)

    Google Scholar 

  33. H. Temimi, A. Ansari, A semi analytical iterative technique for solving nonlinear problems. J. Comput. Math. Appl. 61, 203–210 (2011)

    MathSciNet  MATH  Google Scholar 

  34. N. Herisanu, V. Marinca, Accurate analytical solutions to oscillators with discontinuities and fractional-power restoring force by means of the optimal homotopy asymptotic method. Comput. Math. Appl. 60, 1607–1615 (2010)

    MathSciNet  MATH  Google Scholar 

  35. N. Herisanu, V. Marinca, Explicit analytical approximation to large-amplitude non-linear oscillations of a uniform cantilever beam carrying an intermediate lumped mass and rotary inertia. Meccanica 45, 847–855 (2010)

    MathSciNet  MATH  Google Scholar 

  36. V. Marinca, N. Herisanu, I. Nemes, Optimal homotopy asymptotic method with application to thin film flow. Cent. Eur. J. Phys. 6(3), 648–653 (2008)

    Google Scholar 

  37. N. Herisanu, V. Marinca, T. Dordea, G. Madescu, A new analytical approach to nonlinear vibration of an electric machine. Proc. Roman. Acad. Ser. A: Math. Phys. Technol. Sci. Inf. Sci. 9(3), 229–236 (2008)

    Google Scholar 

  38. V. Marinca, N. Herisanu, C. Bota, B. Marinca, An optimal homotopy asymptotic method applied to the steady flow of fourth-grade fluid past a porous plate. Appl. Math. Lett. 22(2), 245–251 (2009)

    MathSciNet  MATH  Google Scholar 

  39. J.R. Cannon, D.J. Galiffa et al., A numerical method for a nonlocal elliptic boundary value problem. J. Integr. Equ. Appl. 20(2), 243–261 (2008)

    MathSciNet  MATH  Google Scholar 

  40. J.R. Cannon, D.J. Galiffa, On a numerical method for a homogeneous, nonlinear, nonlocal, elliptic boundary value problem. Nonlinear Anal.: Theory Methods Appl. 74(5), 1702–1713 (2011)

    MathSciNet  MATH  Google Scholar 

  41. W. Themistoclakis, A. Vecchio, On the numerical solution of some nonlinear and non-local boundary value problems. Appl. Math. Comput. 255, 135–146 (2015)

    MathSciNet  MATH  Google Scholar 

  42. A. Jafarimoghaddam, On the homotopy analysis method (HAM) and homotopy perturbation method (HPM) for a nonlinearly stretching sheet flow of Eyring-Powell fluids. Int. J. Eng. Sci. 22, 439–451 (2019)

    Google Scholar 

  43. A. Jafarimoghaddam, Two-phase modeling of three-dimensional MHD porous flow of upper-convected Maxwell (UCM) nanofluids due to a bidirectional stretching surface: homotopy perturbation method and highly nonlinear system of coupled equations. Int. J. Eng. Sci. 21, 714–726 (2018)

    Google Scholar 

  44. M.H. Tiwanaa, K. Maqbool, A.B. Mann, Homotopy perturbation Laplace transform solution of fractional non-linear reaction diffusion system of Lotka–Volterra type differential equation. Int. J. Eng. Sci. 20, 672–678 (2017)

    Google Scholar 

  45. M.G. Sobamowo, A.T. Akinshilo, On the analysis of squeezing flow of nanofluid between two parallel plates under the influence of magnetic field. Alex. Eng. J. 57, 1413–1423 (2018)

    Google Scholar 

  46. I. Ullah, H. Khan, M.T. Rahim, Approximation of first grade MHD squeezing fluid flow with slip boundary condition using DTM and OHAM. Math. Probl. Eng. (2013). https://doi.org/10.1155/2013/816262

    Article  MathSciNet  MATH  Google Scholar 

  47. M. Qayyum, H. Khan, M.T. Rahim, I. Ullah, Modeling and analysis of unsteady axisymmetric squeezing fluid flow through porous medium channel with slip boundary. PLoS ONE 10(3), e0117368 (2015)

    Google Scholar 

  48. M.A. AL-Jawary, A semi-analytical iterative method for solving nonlinear thin film flow problems. Chaos Solitons Fract. 99, 52–56 (2017)

    ADS  MathSciNet  MATH  Google Scholar 

  49. J. Ali, S. Islam, S. Islam, G. Zamand, The solution of multipoint boundary value problems by the optimal homotopy asymptotic method. Comput. Math. Appl. 59, 2000–2006 (2010)

    MathSciNet  MATH  Google Scholar 

  50. M. Esmaeilpour, D.D. Ganji, Solution of the Jeffery–Hamel flow problem by optimal homotopy asymptotic method. Comput. Math. Appl. 59, 3405–3411 (2010)

    MathSciNet  MATH  Google Scholar 

  51. L. Ali, S. Islam, T. Gul, I. Khan, L.C.C. Dennis, New version of optimal homotopy asymptotic method for the solution of nonlinear boundary value problems in finite and infinite intervals. Alex. Eng. J. 55, 2811–2819 (2016)

    Google Scholar 

  52. M.S. Hashmi, N. Khan, S. Iqbal, Optimal homotopy asymptotic method for solving nonlinear Fredholm integral equations of second kind. Appl. Math. Comput. 218, 10982–10989 (2012)

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Education, Erciyes University, 38039, Melikgazi, Kayseri, Turkey

    Onur Alp İlhan

Authors
  1. Onur Alp İlhan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Onur Alp İlhan.

Ethics declarations

Conflicts of interest

The authors have declared no conflict of interest

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

İlhan, O.A. Approximation solution of the squeezing flow by the modification of optimal homotopy asymptotic method. Eur. Phys. J. Plus 135, 745 (2020). https://doi.org/10.1140/epjp/s13360-020-00713-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-020-00713-0

Search

Navigation