Sine Function in Trigonometry

Sine Function in Trigonometry: Sine Function is one of the six trigonometric ratios which can be defined as the ratio of perpendicular to the hypotenuse in any right angle triangle.

As we know, trigonometry is the branch of mathematics that deals with the relationship between the side and angle of any right-angle triangle. In modern-day, trigonometry is used beyond the right-angle triangle, such as in fields like physics, engineering, computer graphics, and astronomy, and even in everyday applications like GPS navigation and architectural design, so is the Sine Function.

In this article, we will discuss the definition, formula, and various values of the Sine Function, as well as key properties like domain and range, period, and the graph of the Sine Function.

What is Sine Function?

The sine function is one of the primary trigonometric functions others being tan x, cos x, sec x, cot x, and cosec x.

People often confuse the sine function with the sign. It is important to note that these two are two different things one is function [Sine Function] and the other is polarity of any number [Sign] of function. Generally, we define the Sine function for an angle (say x) and denote it as Sin(x) where x can be measured in radians or degrees.

Sine Function Definition

For an acute angle, It can be defined as the ratio of the opposite side of right triangle to the hypotenuse.

Sine Function Formula

If we suppose a right-angled triangle, then for an angle theta we define sin(θ) as:

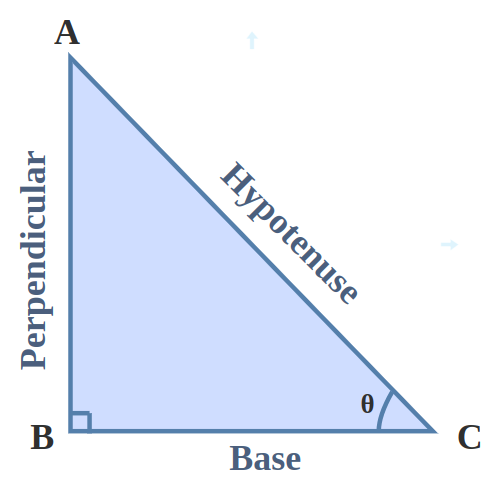
Sin(θ)= Perpendicular or Opposite Side /Hypotenuse

Domain and Range Of Sine Function

The domain of sine function can be defined between all real numbers as sin x is defined for all x in (-∞, ∞). The range of sin x can be defined as [-1, 1] this can be justified as sin x is a ratio and ratio can never exceed 1. The graph of sine function looks like a wave that oscillates between -1 and 1.

• Domain = All real numbers (−∞, ∞)
• Range = [-1, 1]

Period of Sine Function

Since Sine function is a periodic function, we can define the time period after which the values of Sine function begin to repeat. The period of Sine function is 2π and can be written as:

sin (2nπ + x) = sin x n ∈ integer

For instance, sin(2π) = 0. If you add 2π to the ​x, you get sin(2π + 2π), which is sin(4π). Just like sin(2π), sin(4π) = 0. Every time you add or subtract 2π from our ​x​-value, the solution will be the same.

Reciprocal Of Sine Function

The reciprocal of sine function is called cosecant. We can write it as:

1/sin(x) = cosec(x)

OR

cosec(x) = Hypotenuse/Opposite

The product of the reciprocal of sine and the sine function is always equal to 1 which means:

cosec(x) × sin(x) = 1

From the formula of cosec(x), we can note that cosec(x) will be defined for all values of x except where sin(x) is 0, so we can define domain and range of reciprocal of sin(x) as:

• Domain is all real numbers except nπ, where n is an integer.
• The range of the reciprocal of sine is (-∞, -1] U [1, +∞).

Sine Function Graph

The graphical representation of Sine Function:

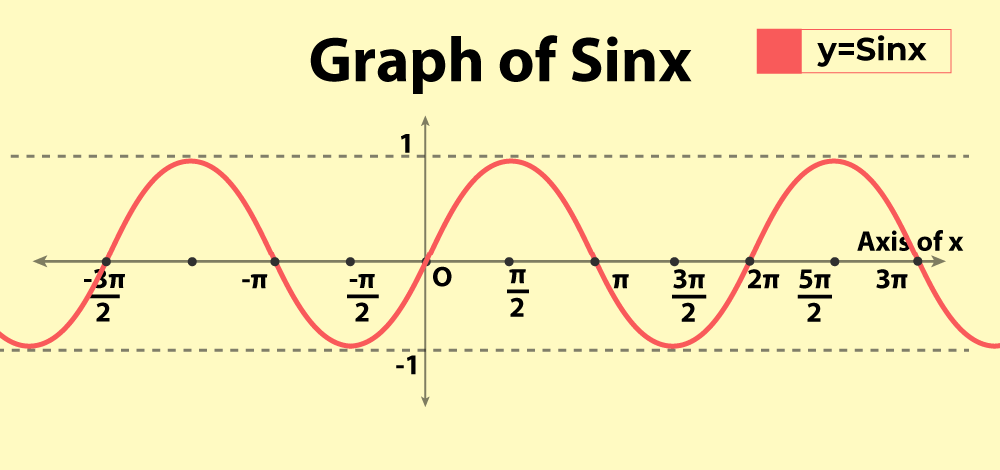
We can see that Sine is a periodic function which repeats after 2π. The function starts from 0, attains a maximum value of +1 at π/2 until it reaches a the value of 0 at π. It further attains a minima -1 at 3π/2 until it reaches the value 0 at 2π and starts repeating the cycle again. The graph represents an odd function. This means sin(-x)=-sin(x).

The periodicity of the graph is 2π.

Derivative of Sine Function

The derivative of the sine function, denoted as sin (x), with respect to x is the cosine function, denoted as cos(x). In mathematical notation, this relationship is expressed as:

d/dx(sin (x)) = cos (x)

So, if you have a function y = sin (x), then the derivative dy/dx is equal to cos (x). This is a fundamental trigonometric identity in Calculus.

Integral of Sine Function

The integral of the sine function, denoted as sin (x), with respect to x is the negative cosine function, denoted as – cos (x), plus a constant of integration. In mathematical notation, this relationship is expressed as:

∫ sin (x) dx = – cos (x) + C

Here, C is the constant of integration, and it represents an arbitrary constant that can take any real value. When you differentiate – cos (x) + C with respect to x, you get sin (x), verifying the relationship.

Sine Function Values Table

The value associated with each value of θ is given in the table:

Angle(θ in Degrees)	Angle(θ in Radians)	Sin(θ)
0°	0	0
30°	π/6	1/2
45°	π/4	1/√2
60°	π/3	√3/2
90°	π/2	1
120°	2π/3	√3/2
135°	3π/4	1/2
180°	π	0
270°	3π/2	-1
360°	2π	0

Other Sine Function Values

Sine 1 Degree is 0.84	Sine 2 Degree is 0.91
Sine 5 Degree is -0.96	Sine 10 Degree is -0.54
Sine 20 Degree is 0.91	Sine 30 Degree is -0.99
Sine 40 Degree is 0.75	Sine 50 Degree is -0.26
Sine 70 Degree is 0.77	Sine 80 Degree is -0.99
Sine 100 Degree is -0.50	Sine 105 Degree is -0.97
Sine 210 Degree is 0.47	Sine 240 Degree is 0.95
Sine 330 Degree is -0.13	Sine 350 Degree is 0.95

Properties of Sine Function

Various properties of Sin Function are:

• It is a periodic function with periodicity of 2π. It means the value of function begins to repeat after an interval of 2π.
• It represents an odd function. This means sin(-x)=-sin(x) and can be confirmed from the graph.
• In a unit circle, sin(θ) is equal to the y coordinate of your point, and cos(θ) is equal to the x-coordinate.
• The range of this function is from [-1,1]. This is the value range over which function can oscillate.
• The domain of the function is [-∞,∞] i.e it is defined for all values of angle.
• Derivative of sin(x) is cos(x).
• Integration of sin(x) is -cos(x).

Inverse Sine Function

The inverse of a trigonometric function gives an inverse trigonometric function. So inverse of sine function is called arcsin.

We can represent it mathematically as “sin^-1 (x)” or “arcsin x”.

We call f^-1 an inverse function of f if f(x)=y ⇒ x=f^-1(y)

So sin x = y ⇒ x = sin^-1(y).

We know that the inverse of a function exists if and only if it is bijective and the domain and range of a function are interchanged to be the range and domain of its inverse function respectively. Hence,

• the domain of sin inverse x is [-1, 1]
• the range of sin inverse x is [-π/2, π/2].

Inverse Sine Function Table

x	y = sin-1(x)
-1	-π/2
-0.5	-π/6
0	0
0.5	π/6
1	π/2

Hyperbolic Sine Function

Hyperbolic sine function is represented by sinh. We use euler’s constant(e) to represent the hyberbolic function. Unlike general sine functions which are represented by a circle of unit radius, hyperbolic functions are represented using a hyperbola.

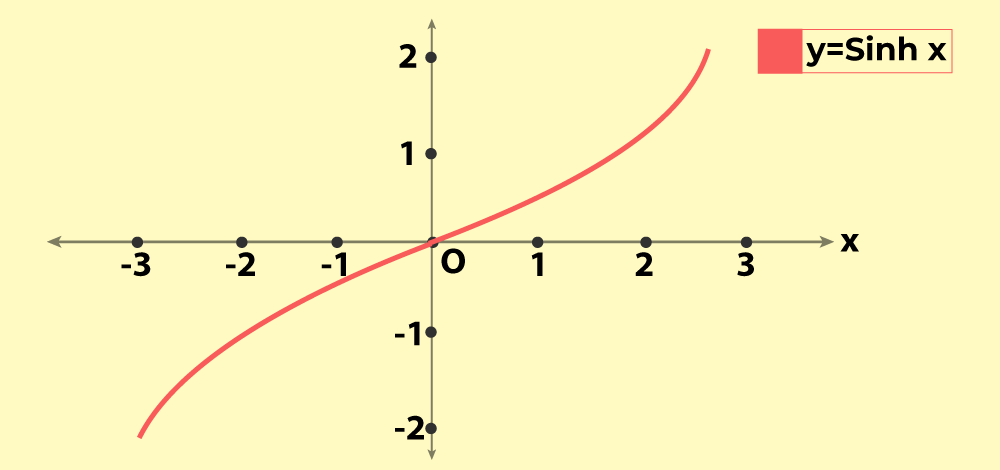
The hyperbolic sine function is a function f: R → R is defined by f(x) = [e^x– e^-x]/2 .

The domain of the sinh(x) function is all real numbers, and the range is (-∞, ∞).

Sine Function Identities

Here is list of Sine function identities which can be used to ease the calculation:

• Sin θ = 1/Cosec(θ)
• sin²θ + cos²θ = 1
• Sin (-θ) = – Sin θ
• Sin (90 – θ) = Cos θ
• sin (180°- θ) = sinθ
• sin(A+B) = sin(A).cos(B)+cos(A).sin(B)
• sin(A–B) = sin(A).cos(B)–cos(A).sin(B)
• sin 2θ = 2 sinθ cosθ
• Sin A + Sin B = 2 Sin(A+B)/2 . Cos(A-B)/2
• Sin A – Sin B = 2 Cos(A+B)/2 . Sin(A-B)/2
• Sin A. Sin B = [Cos (A – B) – Cos (A + B)]/2

Law of Sine in Trigonometry

We have a very important law in mathematics which is used widely in trigonometry. This law is used to calculate the ratio of length of side and sin of angle opposite to that side in a triangle. It can be written as:

a/Sin(A)= b/Sin(B) = c/Sin(C)

This law can be used to calculate the length of a missing side or an angle. It is also called as Sine Rule, Sine Law or Sine Formula.

Sin and Cosine Function

We want to know how does sine and cosine function vary at different values of input angle so here we compare the value of sine and cosine function for most values of angle.

Angle	Sin(θ)	Cos(θ)
0°	0	1
30°	1/2	√3/2
45°	1/√2	1/√2
60°	√3/2	1/2
90°	1	0
120°	√3/2	-1/2
150°	1/2	-√3/2
180°	0	-1
270°	-1	0
360°	0	1

Sine Function Examples

Example 1: Find the value of sin (30°).

Solution:

sin(30°) = sin(π/6 radians)

sin(π/6) is a commonly known value, which is equal to 1/2.

So, sin(30°) = 1/2.

Example 2: Find the value of sin(π/3).

Solution:

sin(π/3) is also a commonly known value, which is equal to √3/2.

Example 3: If sin(x) = 0.8, find the value of x in degrees.

Solution:

To find the value of x, we can take the inverse sine (arcsin) of 0.8:

x = arcsin(0.8)

Using a calculator or table of trigonometric values, you can find that arcsin(0.8) is approximately 53.13°.

Example 4: If sin(2θ) = 0.6 and θ is in the first quadrant, find the value of θ in radians.

Solution:

To find the value of θ, we need to first find the value of 2θ. We can use the inverse sine function:

2θ = arcsin(0.6)

Now, find θ by dividing both sides by 2:

θ = (1/2) × arcsin(0.6)

Using a calculator, you can determine that arcsin(0.6) is approximately 36.87 degrees. So,

θ ≈ (1/2) × 36.87 ≈ 18.44°.

Example 5: Calculate the value of sin(75°) without calculator.

Solution:

We can use the identity sin (x+y) = sin x cos y + sin y cos x

Where x=30° and y=45°

On putting values, we get

sin (75°) = 0.9659

Example 6: If sin(α) = 0.5 and cos(β) = 0.8, find sin(α + β).

Solution:

To find sin(α + β), you can use the sum of angles formula for sine:

sin(α + β) = sin(α) × cos(β) + cos(α) × sin(β)

Using the given values:

⇒ sin(α + β) = 0.5 × 0.8 + √(1 – 0.5²) × √(1 – 0.8²)

⇒ sin(α + β) = 0.4 + √(1 – 0.25) × √(1 – 0.64)

⇒ sin(α + β) = 0.4 + √(0.75) × √(0.36)

⇒ sin(α + β) = 0.4 + 0.866 × 0.6

⇒ sin(α + β) ≈ 0.4 + 0.5196

⇒ sin(α + β) ≈ 0.9196

So, sin(α + β) is approximately 0.9196.

Example 7: An electrician is climbing a 40 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 60°.

Solution:

We notice that the figure will be of a right-angled triangle with rope as hypotenuse , vertical pole as perpendicular .

So sin (60°) = Perpendicular/Hypotenuse

Thus, Height of Pole= 0.87 × 40 = 34.8 m [sin (60°) = 0.87]

Practice Problems on Sine Function in Trigonometry

Problem 1: In △ABC, right-angled at B, if sin(A)=5/13. If the hypotenuse of the triangle is 13 in, then what is the length of the base of the triangle?

Problem 2: Calculate value of sin(135°) using trigonometric identities.

Problem 3: Find all values in range [π,5π] where sin(x)=1/2.

Problem 4: A boat is attached to an anchor which is 50m long and creates a line that is the hypotenuse of a right triangle. It makes an angle between the hypotenuse and the ocean floor that is 25°. So, what will be the depth of the anchor?

Problem 5: Find two values x, y in range [0,π] each such that sin of x+y is 0.96592582628.

FAQs on Sine Function in Trigonometry

What is Sine Function in Trigonometry?

Sine function is equal to the ratio of perpendicular and hypotenuse of a right triangle.

Is Sine Function even or odd?

Sine function is an odd function.

What is the Period of the Sine Function?

The period of sine function is 2π.

How to Graph Sine Function?

Draw a table of values and carefully mark the y values corresponding to each x. Then smoothly connect all the dots giving you a graph.

How to Find the Period of Sine Function?

We can plot the graph of sine function and find the time after values begin to repeat.

What is Amplitude of Sine Function?

It is the vertical distance from the top of a peak to the centre line.

What is the Value of sin 0°?

From the table of values , we can see sin(0)=0.

What is the Value of Sin 30°?

From the table of values , we can see sin(30)=1/2.

What is the Value of Sin 60°?

From the table of values , we can see sin(60)=√3/2.

What is the Domain of Sine Function?

The domain of sine function is all real numbers.

What is the Range of Sine Function?

The range of sine function is [-1,1].