---

Was besagt das Flächenträgheitsmoment?

Das Flächenträgheitsmoment (auch axiales Flächenträgheitsmoment genannt) gibt an, wie schwer es ist, einen Querschnitt zu verbiegen. Ein Sprungbrett im Schwimmbad hat beispielsweise ein sehr kleines Flächenträgheitsmoment. Schließlich muss ein Sprungbrett per Definition beim Aufspringen (also bei Biegung) nachgeben.

---

Tabelle der Flächenträgheitsmomente

Querschnitt	Flächenträgheitsmomente
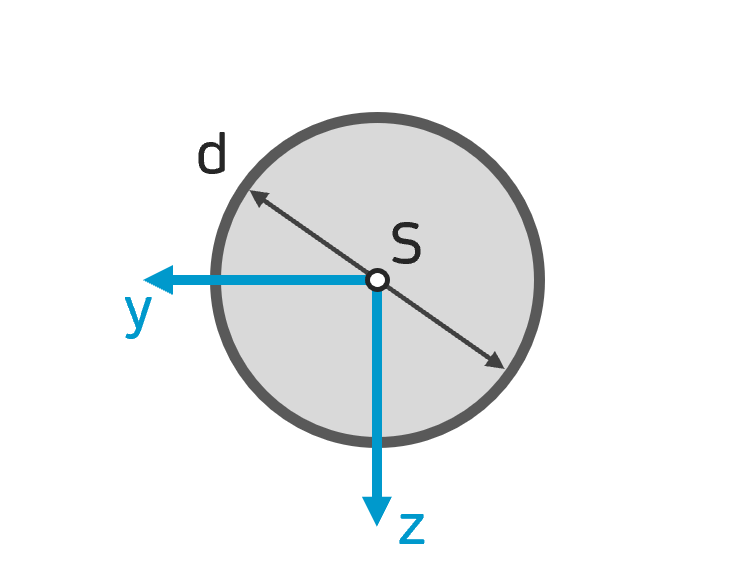Flächenträgheitsmoment Kreis	$$ I_y = I_z = \frac{\pi}{64}d^4 $$ $$ I_{yz} = 0 $$
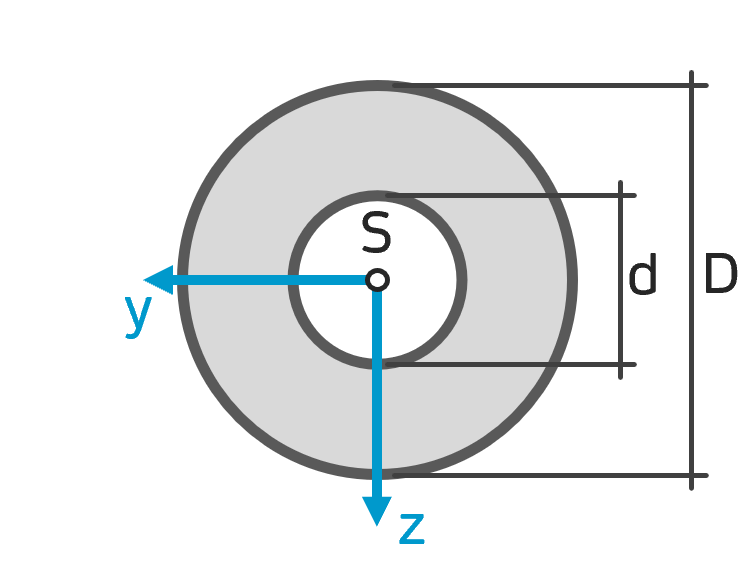Flächenträgheitsmoment Hohlwelle (Hohlprofil)	$$ I_y = I_z = \frac{\pi}{64}(D^4 -d^4)$$ $$ I_{yz} = 0 $$
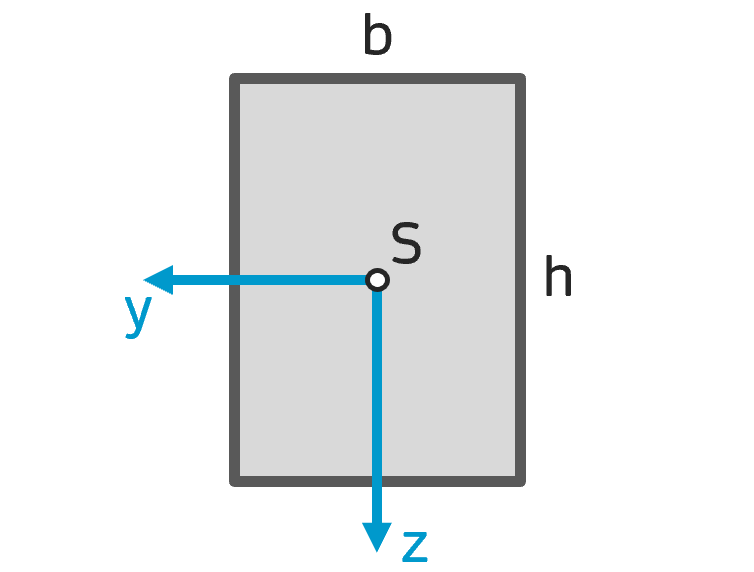Flächenträgheitsmoment Rechteck	$$ I_y = \frac{b h^3}{12} $$ $$ I_z = \frac{h b^3}{12} $$ $$ I_{yz} = 0 $$
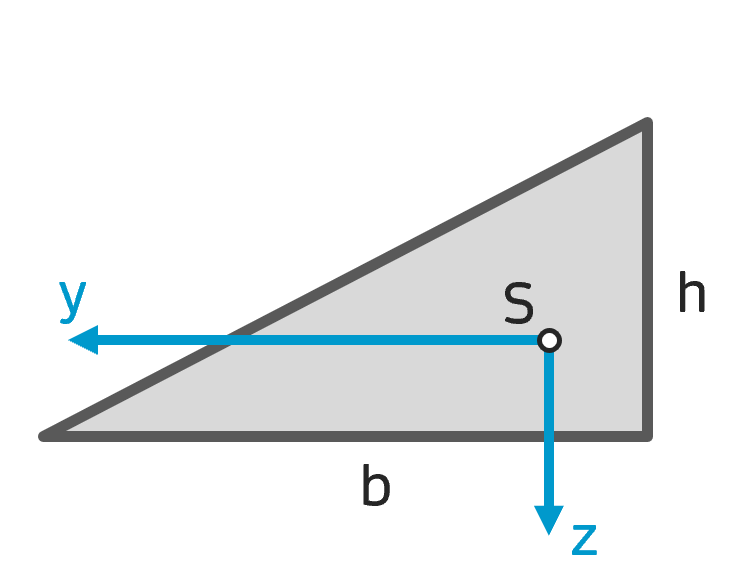Flächenträgheitsmoment rechtwinkliges Dreieck	$$ I_y = \frac{b h^3}{36} $$ $$ I_z = \frac{b^3 h}{36} $$ $$ I_{yz} = \frac{-b^2 h^2}{72} $$
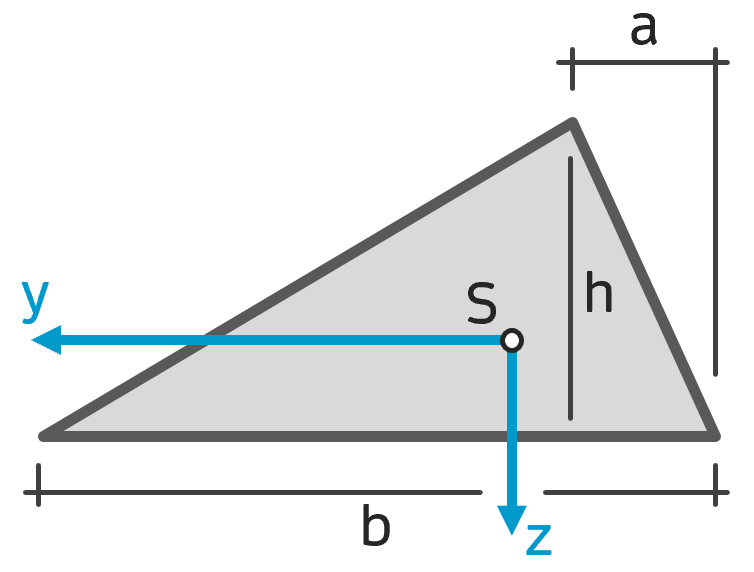Flächenträgheitsmoment allgemeines Dreieck	$$ I_y = \frac{b h^3}{36} $$ $$ I_z = \frac{b h}{36}(b^2 – b a + a^2) $$ $$ I_{yz} = \frac{-b h^2}{72} (b-2a) $$
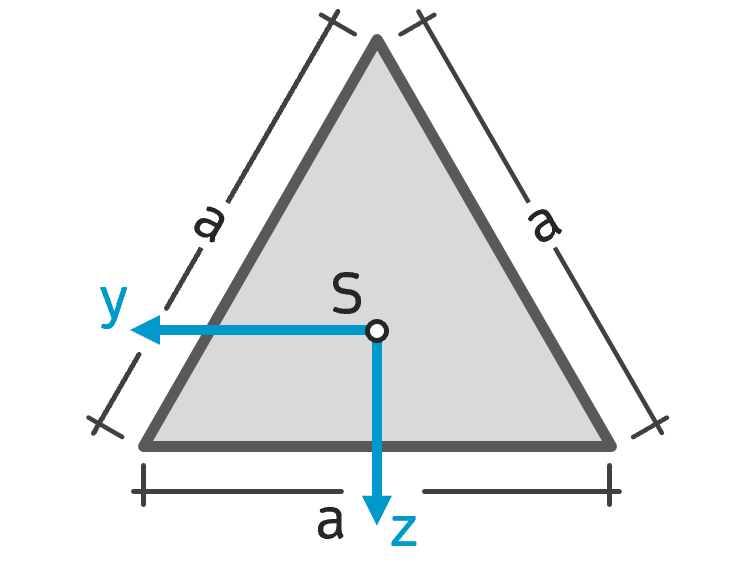Flächenträgheitsmoment gleichseitiges Dreieck	$$ I_y = I_z = \frac{ \sqrt{3} }{ 96 } a^4 $$ $$ I_{yz} = 0 $$
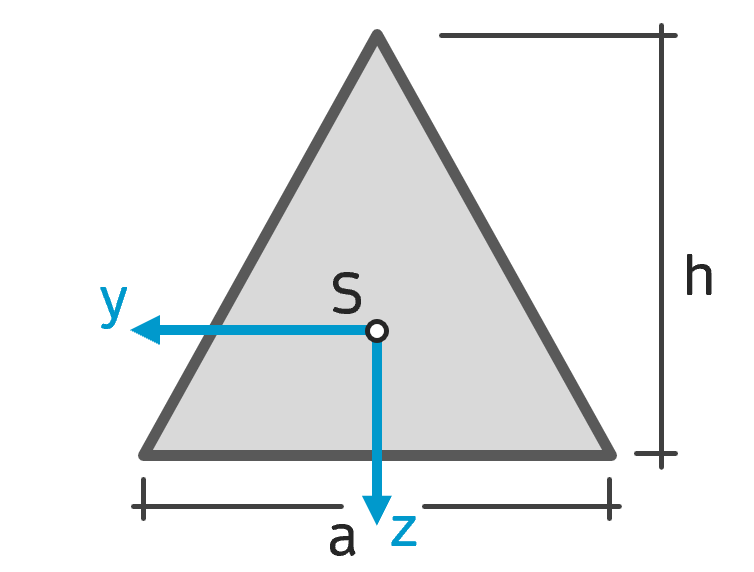Flächenträgheitsmoment gleichschenkliges Dreieck	$$ I_y = \frac{b h^3}{36} $$ $$ I_z = \frac{b^3 h}{48} $$ $$ I_{yz} = 0 $$
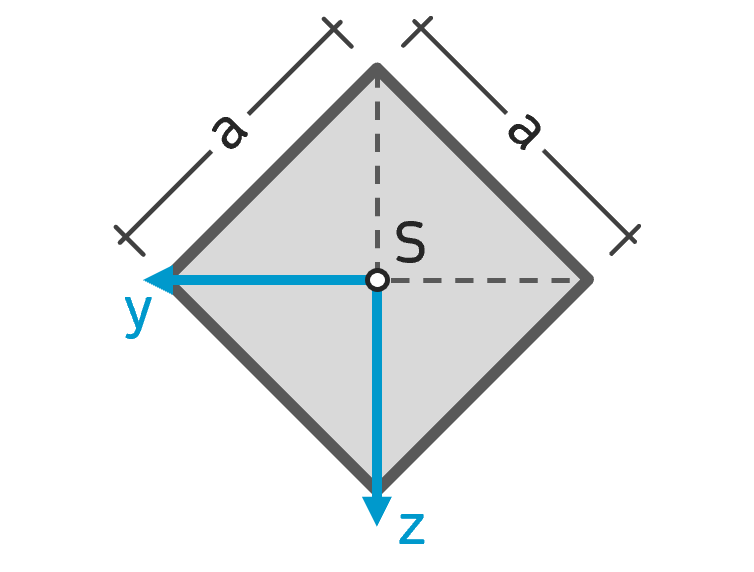Flächenträgheitsmoment Quadrat (45° gedreht)	$$ I_y = I_z = \frac{a^4}{12} $$ $$ I_{yz} = 0 $$
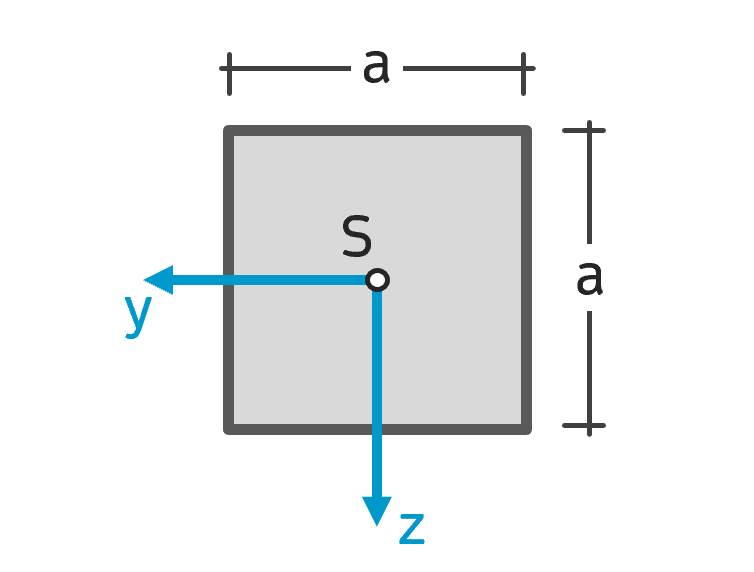Flächenträgheitsmoment Quadrat	$$ I_y = I_z = \frac{a^4}{12} $$ $$ I_{yz} = 0 $$
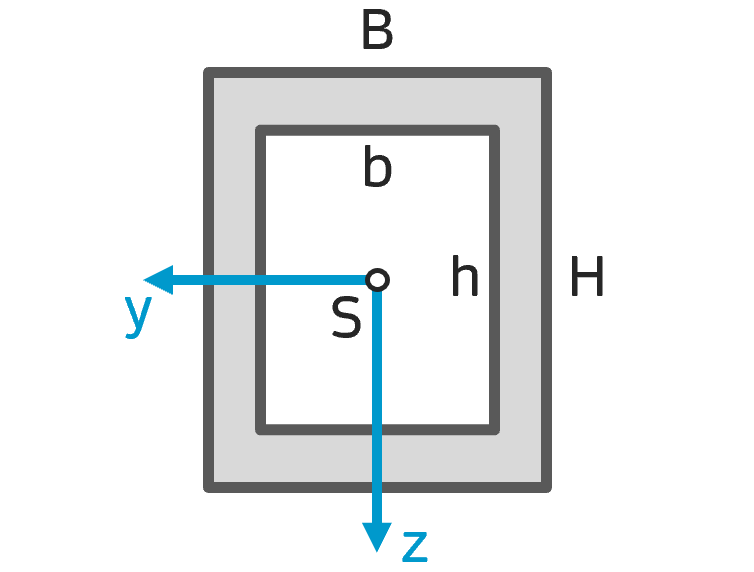Flächenträgheitsmoment Rechteckrohr (Hohlprofil)	$$ I_y = \frac{B H^3 – b h^3}{12} $$ $$ I_z = \frac{B^3 H – b^3 h}{12} $$ $$ I_{yz} = 0 $$
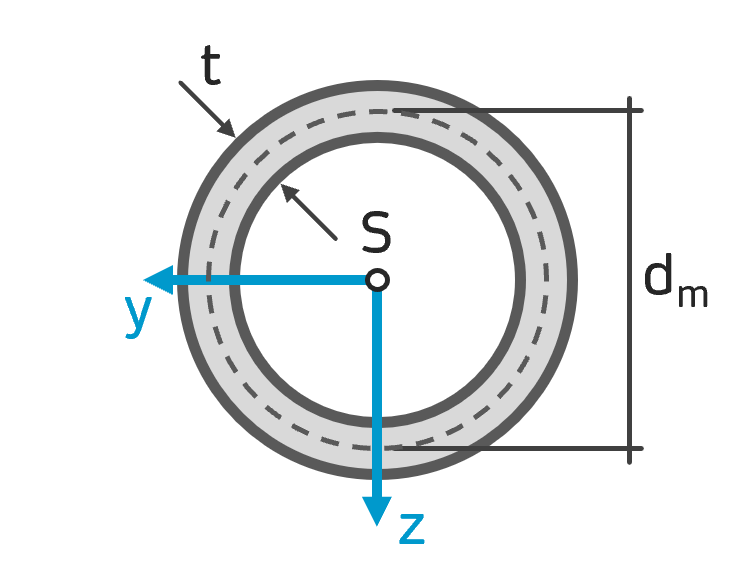Flächenträgheitsmoment dünnwandiges Rohr	$$ I_y = I_z = \frac{\pi}{8}d_m t $$ $$ I_{yz} = 0 $$ Geringe Wanddicke: \( t \ll d_m \)
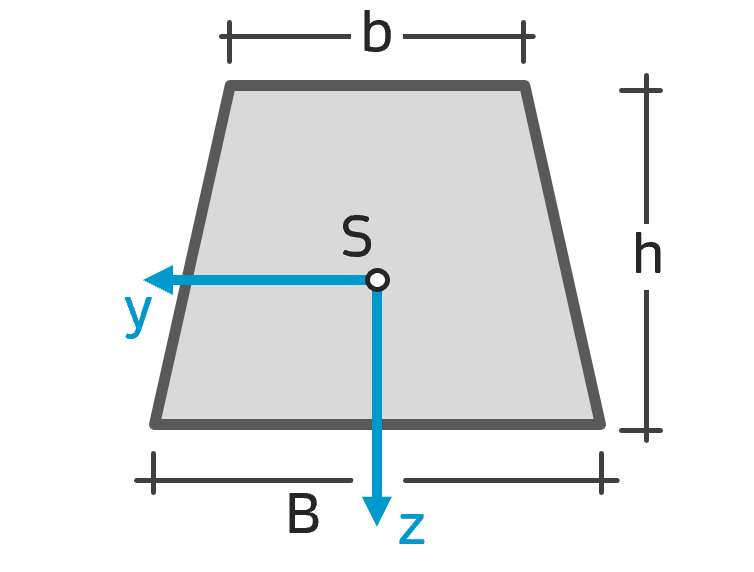Flächenträgheitsmoment Trapez	$$ I_y = \frac{h}{36} \cdot \frac{B^2+4Bb+b^2}{B+b}$$ $$ I_{yz} = 0 $$
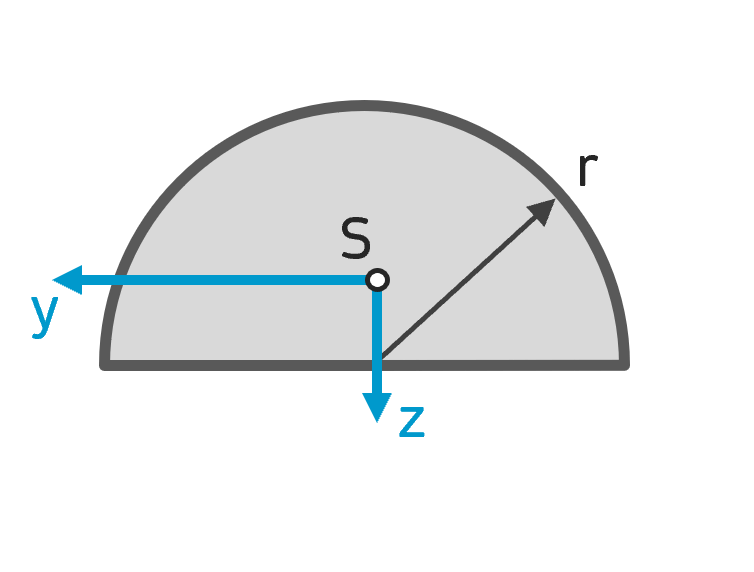Flächenträgheitsmoment Halbkreis	$$ I_y = \left ( \frac{\pi}{8} – \frac{8}{9 \pi} \right ) r^4 \approx 0,1098r^4 $$ $$ I_z \approx 0,392 r^4 $$ $$ I_{yz} = 0 $$
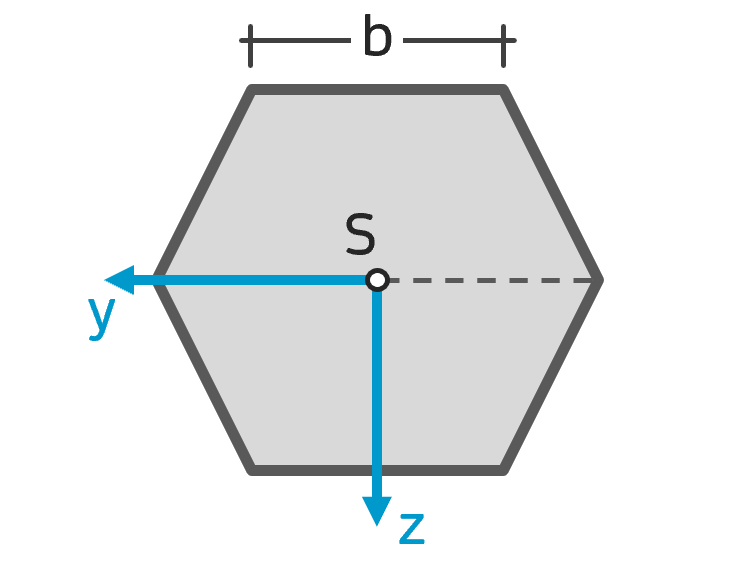Flächenträgheitsmoment Sechseck (Hexagon)	$$ I_y = I_z = \frac{5 \sqrt{3} }{16} b^4 \approx 0,541 b^4 $$ $$ I_{yz} = 0 $$
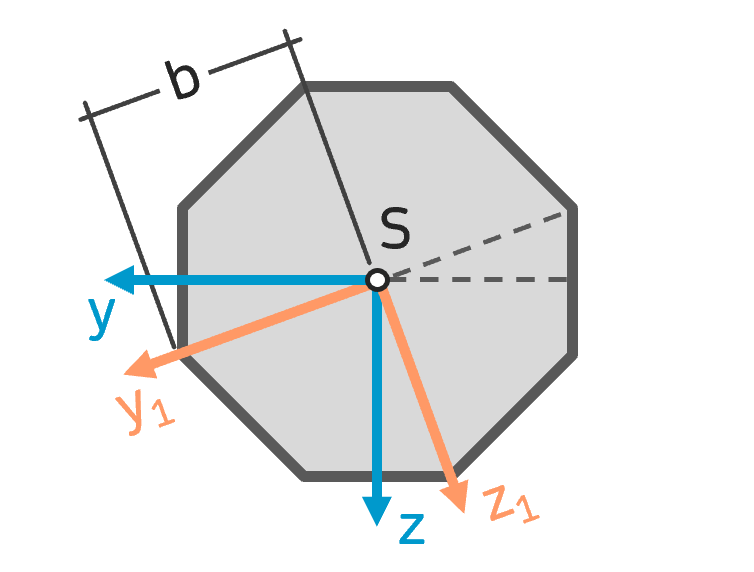Flächenträgheitsmoment Achteck (Oktagon)	$$ I_y = I_z = \frac{1+2 \sqrt{2} }{6} b^4 \approx 0,638b^4 $$ $$ I_{y1} = I_{z1} = \frac{1+2 \sqrt{2} }{6} b^4 \approx 0,638b^4 $$ $$ I_{yz} = I_{yz1} = 0 $$

Hier geht’s zur Tabelle der Flächenschwerpunkte (Schwerpunkte), die für den Steiner Anteil relevant sind. Ein vollständiges Rechenbeispiel mit ausführlichem Lösungsweg ist hier zu finden: Flächenträgheitsmoment berechnen

---

FAQ: Flächenträgheitsmomente

Wie berechnet man das Flächenträgheitsmoment?

Das Flächenträgheitsmoment wird in der Technischen Mechanik üblicherweise mit Hilfe der Flächenträgheitsmoment Tabelle bestimmt. Das liegt daran, dass bei technischen Anwendungen häufig gleiche Querschnittsformen verwendet. Im Maschinenbau hat man beispielsweise oft eine Maschinenwelle mit einem kreisrunden Querschnitt. Bei den Bauingenieuren hat man oft Betonplatten mit einem rechteckigen Querschnitt. Für diese standardisierten Querschnittsformen kann man die fertigen Formeln aus der Tabelle benutzen. Siehe ausführliches Rechenbeispiel: Flächenträgheitsmoment berechnen (Beispielaufgabe)

---

Welche Einheit hat das Flächenträgheitsmoment?

Das Flächenträgheitsmoment hat die Einheit \( m^4 \) (“Meter hoch vier”). Im Maschinenbau wird häufig \( mm^4 \) und bei den Bauingenieuren und Architekten \( cm^4 \) verwendet.

---

Was ist das Flächenträgheitsmoment?

Gute Frage! Das Flächenträgheitsmoment ist ein Maß für den Widerstand eines Querschnitts bei Biegung. Mit anderen Worten: Wie groß ist der Widerstand eines Körpers, wenn man versucht, ihn zu verbiegen. Nun, das hängt einerseits vom Werkstoff (Gummi kann man leichter verbiegen als Stahl) und andererseits vom Querschnitt des Körpers ab. Je dicker der Querschnitt ist, desto schwieriger ist es, den Balken zu verbiegen.

---

Was ist das Deviationsmoment?

Ausgezeichnete Frage! Die Kurzfassung ist: Das Deviationsmoment (oder Zentrifugalmoment) ist in der Festigkeitslehre ein Maß für das Bestreben eines Querschnitts, bei Biegung die Biegeachse zu verändern. Man stelle sich dazu einen eingespannten Balken vor, der ein rechtwinkliges Dreieck als Querschnittsform hat (siehe rechtwinkliges Dreieck in der o. g. Tabelle). Versucht man nun den Balken um die y-Achse zu verbiegen, wird man einerseits festellen, dass der Balken verbogen wird. Andererseits wird man feststellen, dass sich der Querschnitt zusätzlich verdrehen möchte. Dieser Effekt wird durch das Deviationsmoment beschrieben. Ist das Deviationsmoment null, so hat der Querschnitt kein Bestreben, sich bei Biegung zu verdrehen. Das ist bei symmetrischen Querschnitten stets der Fall.

---

Wie berechnet man das Flächenträgheitsmoment bei zusammengesetzten Flächen?

Wenn sich ein Querschnitt aus mehreren Standard-Flächen (Kreis, Rechteck etc.) zusammensetzt, dann kann man mit dem Satz von Steiner das Flächenträgheitsmoment für diesen Querschnitt bestimmen. Das Flächenträgheitsmoment zusammengesetzter Flächen lässt sich dann wie folgt bestimmen:

$$ I_y = \sum I_{y,i} + \sum A_i \cdot b_i^2 $$ $$ I_z = \sum I_{z,i} + \sum A_i \cdot a_i^2 $$ $$ I_{yz} = \sum I_{yz,i} – \sum A_i \cdot b_i \cdot a_i $$

Eine ausführliche Beispielrechnung mit Schritt für Schritt Lösung zeigt, wie man hier vorgehen muss: Flächenträgheitsmoment berechnen bei zusammengesetzten Flächen

---

Video: Flächenschwerpunkt (Steiner-Anteil)

Bei zusammengesetzten Flächen muss der Steiner-Anteil bestimmt werden. Dafür ist es notwendig zu wissen, wo sich der Schwerpunkt der Fläche befindet, um den Steiner-Abstand zu ermitteln. Dieses Video zeigt Schritt für Schritt, wie der Flächenschwerpunkt eines Querschnitts berechnet wird (mit und ohne Tabellenverfahren).

---

Verwandte Themen

Flächenträgheitsmoment berechnen (Beispielaufgabe)
Schwerpunkt berechnen: Prüfungsaufgabe
Oder zurück zur Themenübersicht: Technische Mechanik 1