Pumping Lemma kontextfreie Sprachen Typ2?

m >= 1, d. h. das kürzeste Wort in der Sprache hat die Länge 3m bzw.
|z| = 3n > = n
D. h. wenn mein n = 1 ist, dann hat mein Wort die Länge 3.
Jetzt muss ich eine Aufteilung von |vwx| wählen, dass gilt |vwx| <= n
und dann beim pumpen das Wort Teil meiner Sprache bleibt.
|vwx| <= 1 geht nicht. Macht keinen Sinn, ich muss ja a und b und c einzeln pumpen. a,b,c hat mindestens die Länge 3. Somit macht n = 1 keinen Sinn. n = 2 geht auch nicht. Ich muss mindestens n = 3 wählen. Also z = aaabbbccc nun muss ich |vwx| <= 3 wählen, d. h. ich kann nur 2 von den 3 Symbolen (einzeln) pumpen. ab und c oder a und bc , das macht keinen Sinn.
Fazit:
Man müsste a b c separat (einzeln) pumpen, damit das erzeugte Wort Teil meiner Sprache bleibt, dies ist hier aber nicht möglich egal wie man v und x wählt.
Langt dies als Begründung, oder wie argumentiert man hier am besten?
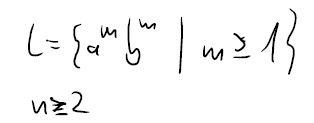
|z| = 2n >=n das kürzeste Wort hat die Länge 2 somit hat auch mein n mindestens die Länge 2.
Wieder muss ich |vwx| so wählen, dass gilt |vwx| <n und beim pumpen dann das Wort Teil meiner Sprache bleibt.
Wie wähle ich nun hier u, v, w, x, y?
2 Antworten

Um die Frage zu beantworten, ist es hilfreich, die Pumping-Lemma-Bedingungen zu berücksichtigen und zu zeigen, dass die Sprache nicht regulär ist.
Erster Fall (|z| = 3n):Du hast festgestellt, dass n = 1 und n = 2 nicht sinnvoll sind. Du kommst zu dem Schluss, dass n = 3 notwendig ist. Jetzt schaust du dir |vwx| <= 3 an. Du argumentierst, dass |vwx| <= 1 nicht sinnvoll ist, weil du a, b und c separat pumpen musst, und sie mindestens die Länge 3 haben. Du kommst zu dem Schluss, dass unabhängig von der Wahl von v und x, es nicht möglich ist, die Bedingungen des Pumping-Lemmas zu erfüllen. Das ist eine gültige Begründung.
Zweiter Fall (|z| = 2n):Du erkennst, dass das kürzeste Wort die Länge 2 hat, und folglich ist n mindestens 2. Du willst nun |vwx| < n wählen. Hier musst du vorsichtig sein, da |vwx| auch 0 sein kann. Die Bedingung |vwx| < n bedeutet, dass |vwx| = 0 oder |vwx| = 1.
- Wenn |vwx| = 0, dann kannst du zeigen, dass keine Zerlegung von z existiert, die die Bedingungen des Pumping-Lemmas erfüllt.
- Wenn |vwx| = 1, dann könntest du argumentieren, dass aufgrund der Struktur von z (2n), es nicht möglich ist, v, w und x so zu wählen, dass das gepumpte Wort in der Sprache bleibt.
Zusammenfassend könntest du argumentieren, dass unabhängig von der Wahl von v, w und x es nicht möglich ist, die Bedingungen des Pumping-Lemmas zu erfüllen.
Die Argumentation könnte durch Hinzufügen von konkreten Beispielen oder weiteren Details gestärkt werden, aber die allgemeine Struktur deiner Begründung ist solide.

ok stopp hab hier mist geschrieben glaube ich
ok bei a^n b^n wird dir ein n gegeben.
einfach vx= das ab in der mitte, rest ist ja dann trivial hoffe ich?
bei a^n b^n c^n wählst du jetzt n=2
dann verkackt dein gegenüber schon bei dem wort der länge 3 also abc
dann kann er ja mit vx nur zu wenig "covern". heißt es werden nicht alle a,b und c gleichmäßig gepumpt. also ist das pumping lemma für a^n b^n c^n nicht erfüllt und es ist somit nicht typ2
oder was meintest du. checks nicht ganz