Endliche Automaten

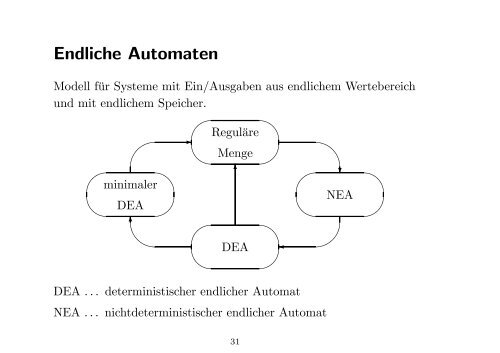
<strong>Endliche</strong> <strong>Automaten</strong><br />

Modell für Systeme mit Ein/Ausgaben aus endlichem Wertebereich<br />

und mit endlichem Speicher.<br />

<br />

<br />

Reguläre<br />

<br />

Menge<br />

<br />

<br />

minimaler<br />

NEA<br />

DEA<br />

<br />

<br />

<br />

DEA <br />

<br />

DEA . . . deterministischer endlicher Automat<br />

NEA . . . nichtdeterministischer endlicher Automat<br />

31

---

Beispiel.<br />

q 4<br />

<br />

<br />

digit <br />

digit <br />

<br />

. <br />

E <br />

digit <br />

digit <br />

<br />

<br />

q0 q1 q2 q3 q5<br />

Deterministischer endlicher Automat (DEA)<br />

digit digit<br />

+, −<br />

Nichtdeterministischer endlicher Automat (ε-NEA)<br />

digit<br />

<br />

digit <br />

digit<br />

<br />

+<br />

<br />

<br />

digit<br />

. <br />

<br />

E<br />

<br />

ε digit<br />

<br />

<br />

q0 q1 q2 q3 − q4 q5<br />

<br />

32

---

Deterministischer endlicher Automat<br />

A = 〈Q, Σ, δ, q 0 , F 〉, wobei<br />

Q . . . endliche Menge von Zuständen<br />

Σ . . . Eingabealphabet<br />

δ: Q × Σ → Q . . . Übergangsfunktion (total)<br />

q 0 ∈ Q . . . Anfangszustand<br />

F ⊆ Q . . . Menge von Endzuständen<br />

Falle: Sei A = 〈Q, Σ, δ, q 0 , F 〉 ein DEA und q ∈ Q − F mit<br />

δ(q, a) = q für alle a ∈ Σ. Dann heißt q Falle.<br />

Zur Erhöhung der Übersichtlichkeit können Fallen bei der<br />

Beschreibung von endlichen <strong>Automaten</strong> weggelassen werden.<br />

33

---

Deterministischer endlicher Automat<br />

Erweiterte Übergangsfunktion: δ ∗ : Q × Σ ∗ → Q<br />

δ ∗ (q, ε) = q, δ ∗ (q, aw) = δ ∗ (δ(q, a), w)<br />

für alle q ∈ Q, w ∈ Σ ∗ , a ∈ Σ.<br />

Akzeptierte Sprache: L(A) = {w ∈ Σ ∗ | δ ∗ (q 0 , w) ∈ F }<br />

34

---

Einschub: Graphen<br />

Seien U und W endliche Mengen. Ein markierter gerichteter Graph<br />

g über U und W ist ein Tripel (K, E, L) wobei<br />

• K die Menge der Knoten<br />

• E ⊆ K × W × K die Menge der Kanten<br />

• L : K → U die Knotenmarkierungsfunktion ist.<br />

Ein Element (x, w, y) ∈ E stellt eine gerichtete Kante vom Knoten<br />

x zum Knoten y mit Markierung w dar.<br />

Zwei markierte gerichtete Graphen g = (K, E, L) und<br />

g ′ = (K ′ , E ′ , L ′ ) über U und W heißen isomorph, wenn wenn es<br />

eine bijektive Abbildung f : K → K ′ gibt, sodass für alle k, l ∈ K<br />

und w ∈ W gilt: (k, w, l) ∈ E genau dann wenn (f(k), w, f(l)) ∈ E ′ .<br />

Gilt außerdem L(k) = L ′ (f(k)) für alle k ∈ K, so heißen g und g ′<br />

äquivalent.<br />

35

---

Minimalautomat<br />

Satz. Zu jeder regulären Sprache kann man effektiv einen DEA mit<br />

einer minimalen Anzahl von Zuständen konstruieren, der bis auf<br />

die Umbenennung der Zustände eindeutig ist.<br />

36

---

Nichtdeterministischer endlicher Automat<br />

Übergangsfunktion NEA: δ: Q × Σ → P(Q)<br />

Übergangsfunktion ε-NEA: δ: Q × (Σ ∪ {ε}) → P(Q)<br />

Erweiterte Übergangsfunktion: δ ∗ : Q × Σ ∗ → P(Q)<br />

δ ∗ (q, w) = {q ′ ∈ Q | q w q ′ }<br />

q w q ′ . . . es gibt einen mit w beschrifteten Pfad von q nach q ′<br />

Akzeptierte Sprache:<br />

L(A) = {w ∈ Σ ∗ | δ ∗ (q 0 , w) ∩ F ≠ {}}<br />

Definition. <strong>Automaten</strong> A und A ′ sind äquivalent, falls<br />

L(A) = L(A ′ ).<br />

37

---

Determinisierung (NEA → DEA)<br />

Satz. Zu jedem NEA gibt es einen äquivalenten DEA.<br />

NEA: A = 〈Q, Σ, δ, q 0 , F 〉<br />

DEA: Â = 〈 ˆQ, Σ, ˆδ, ˆq 0 , ˆF 〉, wobei<br />

ˆQ = P(Q)<br />

ˆδ(ˆq, a) = ⋃ δ ∗ (q, a) für alle ˆq ∈ ˆQ, a ∈ Σ<br />

q∈ˆq<br />

ˆq 0 = {q 0 }<br />

{ {ˆq ∈ ˆQ | ˆq ∩ F ≠ {}} ∪ {ˆq0 } falls ε ∈ L(A)<br />

ˆF =<br />

{ˆq ∈ ˆQ | ˆq ∩ F ≠ {}} sonst<br />

Tipp: Berechne die Übergangsfunktion ausgehend von ˆq 0 nur für<br />

tatsächlich erreichbare Zustände.<br />

38

---

Reguläre Menge → ε-NEA<br />

Satz. Zu jeder regulären Sprache L gibt es einen endlichen<br />

<strong>Automaten</strong> A, sodass L = L(A).<br />

L = {}:<br />

<br />

L = {s}:<br />

s <br />

s ∈ (Σ ∪ {ε})<br />

L = L 1 ∪ L 2 :<br />

<br />

<br />

q0,1<br />

ε<br />

ε<br />

<br />

q0,2<br />

<br />

A 1<br />

A 2<br />

q f,1<br />

q f,2<br />

<br />

<br />

<br />

<br />

<br />

<br />

39

---

o.B.d.A. hat A 1 nur einen Endzustand!<br />

L = L 1 · L 2 :<br />

<br />

A ε<br />

1<br />

<br />

q0,1 q f,1<br />

q0,2<br />

<br />

A 2<br />

q f,2<br />

<br />

<br />

<br />

L = (L 1 ) ∗ :<br />

<br />

<br />

ε<br />

<br />

<br />

<br />

<br />

<br />

<br />

q0,1<br />

ε<br />

A 1<br />

ε<br />

q f,1<br />

<br />

<br />

<br />

ε <br />

<br />

<br />

<br />

<br />

40

---

DEA → reguläre Menge<br />

Satz. Jede von einem DEA akzeptierte Sprache ist regulär.<br />

A = 〈{q 1 , . . ., q n }, Σ, δ, q 1 , F 〉<br />

R k ij . . . Menge aller Wörter, mit denen man von q i nach q j gelangt,<br />

ohne einen Zustand mit einem Index größer als k zu berühren.<br />

R 0 ij =<br />

{ {s ∈ Σ | δ(qi , s) = q j } i ≠ j<br />

{s ∈ Σ | δ(q i , s) = q j } ∪ {ε} i = j<br />

R k ij = R k−1<br />

ij<br />

L(A) = ⋃<br />

q j ∈F<br />

∪ R k−1<br />

ik<br />

R n 1j<br />

· (R k−1<br />

kk<br />

)∗ · R k−1<br />

kj<br />

k > 0<br />

41

---

Beispiel.<br />

<br />

1<br />

<br />

q 1<br />

<br />

<br />

0<br />

0 1 <br />

q 2<br />

q<br />

<br />

3<br />

<br />

<br />

<br />

0, 1<br />

<br />

<br />

<br />

42

---

k = 0 k = 1 k = 2<br />

R11 k {ε} {ε} {00} ∗<br />

R12 k {0} {0} {0} · {00} ∗<br />

R13 k {1} {1} {0} ∗ · {1}<br />

R21 k {0} {0} {0} · {00} ∗<br />

R22 k {ε} {ε, 00} {00} ∗<br />

R23 k {1} {1, 01} {0} ∗ · {1}<br />

R31 k {} {} {0, 1} · {00} ∗ · {0}<br />

R32 k {0, 1} {0, 1} {0, 1} · {00} ∗<br />

R33 k {ε} {ε} {ε} ∪ {0, 1} · {0} ∗ · {1}<br />

43

---

Eigenschaften regulärer Sprachen<br />

L reg (Σ) ist abgeschlossen gegenüber<br />

• Vereinigung, Verkettung, Stern-Operator: per Definition.<br />

• Plus-Operator: A + = A ∗ · A.<br />

• Komplement bzgl. Σ ∗ : konstruiere DEA und vertausche Endund<br />

Nichtendzustände.<br />

• Durchschnitt: A ∩ B = A ∪ B.<br />

• Differenz: A − B = A ∩ B.<br />

• Homomorphismen: Sei h: Σ → Σ ′∗ eine Abbildung von<br />

Symbolen aus Σ auf Wörter über Σ ′ .<br />

Ist L eine reguläre Sprache, dann auch h(L) = {h(w) | w ∈ L}.<br />

Beweis: repräsentiere L durch regulären Ausdruck und ersetze<br />

alle Vorkommnisse von a durch Ausdruck für h(a).<br />

44

---

Homomorphismus<br />

h(ε) = ε, h(wa) = h(w)h(a)<br />

für alle w ∈ Σ ∗ und a ∈ Σ<br />

Beispiel.<br />

h(0) = a und h(1) = bbb<br />

Wenn w = 011 dann<br />

h(w) = abbbbbb.<br />

45

---

Folgende Probleme sind für reguläre Sprachen L, L ′ entscheidbar.<br />

• Gehört ein Wort w der Sprache L an?<br />

Konstruiere einen DEA für L und prüfe δ ∗ (q 0 , w) ∈ F .<br />

• Ist L leer?<br />

Konstruiere einen DEA für L und prüfe, ob von q 0 aus ein<br />

Endzustand erreichbar ist.<br />

• Ist L endlich oder unendlich?<br />

L ist unendlich gdw. der minimale DEA für L (abgesehen von<br />

der Falle!) einen Zyklus enthält.<br />

• Gilt L = L ′ ?<br />

Überprüfe, ob L − L ′ und L ′ − L leer sind.<br />

46

---

Grenzen regulärer Sprachen<br />

Beispiel. Modulo-Arithmetik<br />

L . . . Menge aller binären Numerale ohne führende Nullen, die<br />

kongruent 0 modulo 5 sind<br />

z(x) = durch Darstellung x repräsentierte Zahl.<br />

Beispiel.<br />

z(1000) = 8 = 3 mod 5,<br />

z(10000) = 8 ∗ 2 = 1 mod 5,<br />

z(10001) = 8 ∗ 2 + 1 = 2 mod 5,<br />

Prinzip: Ist z(x) = i mod 5 dann<br />

z(x0) = 2 ∗ i mod 5,<br />

z(x1) = 2 ∗ i + 1 mod 5.<br />

47

---

Zustand i . . . ”<br />

bisherige Zahl ist kongruent i mod 5“<br />

δ(i, 0) = (i · 2 + 0) mod 5<br />

δ(i, 1) = (i · 2 + 1) mod 5<br />

<br />

0 3<br />

<br />

<br />

1 1 0<br />

<br />

1 <br />

<br />

0 <br />

0 <br />

4<br />

1 2<br />

<br />

<br />

1<br />

1<br />

1<br />

<br />

<br />

<br />

0<br />

0<br />

48

---

Beispiel. Geschachtelte Strukturen<br />

Ist L = {a n b n | n ≥ 0} regulär?<br />

Angenommen, es gibt DEA A = 〈Q, Σ, δ, q 0 , F 〉 für L.<br />

Wir betrachten δ ∗ (q 0 , a i ) für i = 1, 2, 3, . . . .<br />

Schubfachprinzip: es gibt m, n sodass<br />

m ≠ n aber δ ∗ (q 0 , a m ) = q = δ ∗ (q 0 , a n ) .<br />

a n b n ∈ L(A), daher gilt δ ∗ (q, b n ) = q f ∈ F .<br />

Wir erhalten:<br />

δ ∗ (q 0 , a m b n ) = δ ∗ (δ ∗ (q 0 , a m ), b n )<br />

= δ ∗ (q, b n )<br />

= q f<br />

d.h., a m b n ∈ L(A) obwohl m ≠ n!<br />

Folgerung: L ist nicht regulär.<br />

49

---

Pumping Lemma für reguläre Sprachen<br />

Sei L eine unendliche reguläre Sprache.<br />

Für alle hinreichend großen Wörter w ∈ L existiert eine Zerlegung<br />

w = xyz mit y ≠ ε, sodass xy i z ∈ L für alle i = 0, 1, 2, . . .<br />

Formal: Es gibt eine (nur von L abhängige) Schranke m > 0, sodass<br />

für alle w ∈ L mit |w| ≥ m gilt:<br />

w kann geschrieben werden als<br />

w = xyz mit |xy| ≤ m und |y| > 0<br />

sodass<br />

w i = xy i z ∈ L für alle i ≥ 0.<br />

50

---

Beispiel. L = {a n b n | n ≥ 0}<br />

Wäre L regulär, müsste Pumping Lemma gelten.<br />

• Lemma gilt für alle w mit |w| ≥ m, m unbekannt.<br />

• Wähle w = a m b m .<br />

• Nachdem |xy| ≤ m und |y| > 0 besteht y aus lauter Symbolen<br />

a, also y = a k für 0 < k < m.<br />

• Betrachte w 0 = a m−k b m .<br />

Da w 0 /∈ L, ist L nicht regulär.<br />

51